Matematica discreta

NOTA: SOLO FALTAN LLENAR TEMAS QUE NO SE HAN VISTO.

UNIDAD V. GRAFOS

5.1 GRAFOS

Un grafo (del griego grafos: dibujo, imagen) es el principal objeto de estudio de la teoría de grafos.

Informalmente, un grafo es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto.

Típicamente, un grafo se representa gráficamente como un conjunto de puntos (vértices o nodos) unidos por líneas (aristas).

5.1.1 NODOS

Un nodo es cada uno de los elementos que una lista enlazada, de un árbol o de un grafo. Cada nodo será una estructura o registro que dispondrá de varios campos, al menos uno de esos campos será un puntero o referencia a otro nodo, de forma que conocido un nodo, a partir de esa referencia, debe poder accederse a otros nodos de la estructura. Los nodos son herramientas esenciales para la construcción de estructuras de datos dinámicas.

5.1.2 RAMAS Y LAZOS

Un lazo o bucle es una arista que relaciona al mismo nodo; es decir, una arista donde el nodo inicial y el nodo final coinciden.

5.1.3 VALENCIA
5.1.4 CAMINO
5.1.5 RAMAS PARALELAS

5.1.6 GRAFOS SIMPLES

Un grafo es simple si a lo sumo sólo 1 arista une dos vértices cualesquiera. Esto es equivalente a decir que una arista cualquiera es la única que une dos vértices específicos.

Un grafo que no es simple se denomina complejo.

5.1.7 GRAFOS DE SIMILARIDAD

5.1.8 GRAFOS BIPARTITOS Y GRAFOS COMPUESTOS

Grafos COMPUESTOS
Un grafo simple es completo si existen aristas uniendo todos los pares posibles de vértices. Es decir, todo par de vértices (a, b) debe tener una arista e que los une.

El conjunto de los grafos completos es denominado usualmente $mathbb{K}$ , siendo $mathbb{K}_n$ el grafo completo de n vértices.

Un K_n, es decir, grafo completo de $n$ vértices tiene exactamente 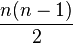$frac{n(n-1)}{2}$ aristas.

La representación gráfica de los K_n como los vértices de un polígono regular da cuenta de su peculiar estructura.

Grafos bipartitos

Un grafo G es bipartito si puede expresarse como $G = {V_1 cup V_2, A}$ (es decir, sus vértices son la unión de dos grupos de vértices), bajo las siguientes condiciones:

$V 1$ y $V 2$ son disjuntos y no vacíos.

Cada arista de A une un vértice de V₁ con uno de V₂.

No existen aristas uniendo dos elementos de V₁; análogamente para V₂.

Bajo estas condiciones, el grafo se considera bipartito, y puede describirse informalmente como el grafo que une o relaciona dos conjuntos de elementos diferentes, como aquellos resultantes de los ejercicios y puzzles en los que debe unirse un elemento de la columna A con un elemento de la columna B.

5.2 REPRESENTACIÓN MATRICIAL DE GRAFOS

5.2.1 RAMAS SUCESIVAS DE LONGITUD “N”

5.2.2 MATRIZ DE ADYACENCIA E INCIDENCIA

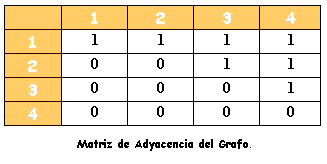
MATRIZ DE ADYACENCIA

Las columnas y filas de la matriz representan los nodos del grafo.

Se llena la matriz de ceros (0).

Por cada arista que une a dos nodos, se suma uno (1) al valor que hay actualmente en la ubicación correspondiente de la matriz.

Si tal arista es un bucle y el grafo es no dirigido, entonces se suma dos (2) en vez de uno (1).

Finalmente, se obtiene una matriz que representa el número de aristas (relaciones) entre cada par de nodos (elementos).

Existe una matriz de adyacencia única para cada grafo (sin considerar las permutaciones de filas o columnas), y viceversa.

GRAFO DIRIGIDO

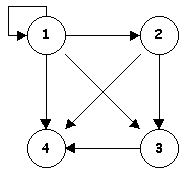
GRAFO NO DIRIGIDO

MATRIZ DE INCIDENCIA

Relación binaria descrita mediante una matriz de incidencia, y mediante un grafo

Las columnas de la matriz representan las aristas del grafo.

Las filas representan a los distintos nodos.

Por cada nodo unido por una arista, ponemos un uno (1) en el lugar correspondiente, y llenamos el resto de las ubicaciones con ceros (0).

En el ejemplo de la figura, si sumamos las cantidades de 1's que hay en cada columna, veremos que hay solo dos. Pero si sumamos las cantidades de unos 1's que hay por cada fila, comprobaremos que los nodos 2, 4 y 5 poseen un valor de 3. Ese valor indica la cantidad de aristas que inciden sobre el nodo.

5.2.3 CAMINO

Un ciclo es un camino, es decir una sucesión de aristas adyacentes, donde no se recorre dos veces la misma arista, y donde se regresa al punto inicial.

5.3 GRAFOS DIRIGIDOS

Un grafo dirigido o digrafo es un grafo $G = (V, E)$ donde:

$Vneqemptyset$

$E subseteq {(a,b) in V times V: a neq b },$ es un conjunto de pares ordenados de elementos de $V,$ .

Dada una arista $(a, b)$ , $a$ es su nodo inicial y $b$ su nodo final.

Por definición, los grafos dirigidos no contienen bucles.

5.4 GRAFOS ISOMORFOS

Dos grafos son isomorfos cuando existe una correspondencia biunívoca (uno a uno), entre sus vértices de tal forma que dos de estos quedan unidos por una arista en común. En si sus tablad de adyacencia son iguales.

5.4.1 TRAYECTORIA Y CIRCUITOS EULERIANOS

5.4.2 TRAYECTORIA Y CIRCUITOS HAMILTONIANOS

5.5 GRAFOS CONEXOS

Un grafo es fuertemente conexo si cada par de vértices está conectado por al menos dos caminos disjuntos; es decir, es conexo y no existe un vértice tal que al sacarlo el grafo resultante sea disconexo.

Es posible determinar si un grafo es conexo usando un algoritmo Búsqueda en anchura (BFS) o Búsqueda en profundidad (DFS).

En términos matemáticos la propiedad de un grafo de ser (fuertemente) conexo permite establecer en base a él una relación de equivalencia para sus vértices, la cual lleva a una partición de éstos en "componentes (fuertemente) conexas", es decir, porciones del grafo, que son (fuertemente) conexas cuando se consideran como grafos aislados. Esta propiedad es importante para muchas demostraciones en teoría de grafos.

5.5.1 CAMINOS DE EULER Y HAMILTON

5.5.2 COMPONENTES DE UN GRAFO

5.6 GRAFOS PONDERADOS

En muchos casos, es preciso atribuir a cada arista un número específico, llamado valuación, ponderación o coste según el contexto, y se obtiene así un grafo valuado.
Formalmente, es un grafo con una función v: A → R₊.

Por ejemplo, un representante comercial tiene que visitar n ciudades conectadas entre sí por carreteras; su interés previsible será minimizar la distancia recorrida (o el tiempo, si se pueden prever atascos). El grafo correspondiente tendrá como vértices las ciudades, como aristas las carreteras y la valuación será la distancia entre ellas.
Y, de momento, no se conocen métodos generales para hallar un ciclo de valuación mínima, pero sí para los caminos desde a hasta b, sin más condición.

5.6.1 LONGITUD DE UN CAMINO

5.6.2 CAMINO MÁS CORTO

El algoritmo de Dijkstra, también llamado algoritmo de caminos mínimos, es un algoritmo para la determinación del camino más corto dado un vértice origen al resto de vértices en un grafo dirigido y con pesos en cada arista. Su nombre se refiere a Edsger Dijkstra, quien lo describió por primera vez en 1959.

La idea subyacente en este algoritmo consiste en ir explorando todos los caminos más cortos que parten del vértice origen y que llevan a todos los demás vértices; cuando se obtiene el camino más corto desde el vértice origen, al resto de vértices que componen el grafo, el algoritmo se detiene.

5.6.3 GRAFOS PLANOS

5.6.4 GRAFOS HOMEOMORFOS

5.7 GRÁFICAS NO DIRIGIDAS

5.7.1 ALGORITMOS PARA GRÁFICAS